MapoGPS
Github: https://github.com/lucasoshiro/MapoGPS.
If you are in São Paulo, please, enable your location, I promise it will be cool!
So… what is this
Until not long ago, Waze and Google Maps didn’t exit, so people had to use paper maps. The city where I live here in Brazil, São Paulo, is a huge city with more than 12 million people, so, a map of this city is so big that needed to be printed as a book. You can see how it looks here (if you don’t speak Portuguese, it is fine to Google Translate it). We call it “guia de ruas”, that literally means “street guide”.
Personally, when I’m driving I don’t like to hear a voice dictating where I should turn, and I don’t feel comfortable with an app deciding where I should go. I also don’t like how the maps are displayed in those apps, I still prefer how the streets are presented in the street guide. So, even though I’m not so old (I was born in 1996), I keep a street guide in my car (the most famous one, Mapograf, that is still published and updated).
So, I wrote this little utility to convert lat/lng coordinates into the page and coordinates of a street map, for the following reasons:
- I was bored;
- I could bring a little bit of technology for something more traditional;
How do we do it?
Street guide coordinate system
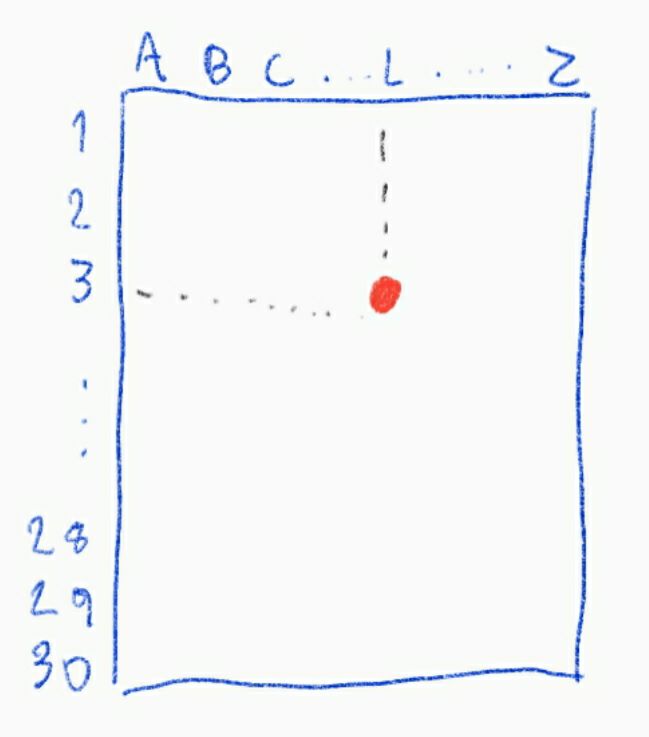
The pages that contain the maps are numbered from A1 to A99, from B1 to B27 and from 1 to 432. Each page has a coordinate system where the lines are numbered from 1 to 30 and the columns are identified from A to Z (with some missing letters…).
Conversion overview
The conversion is done in three steps:
-
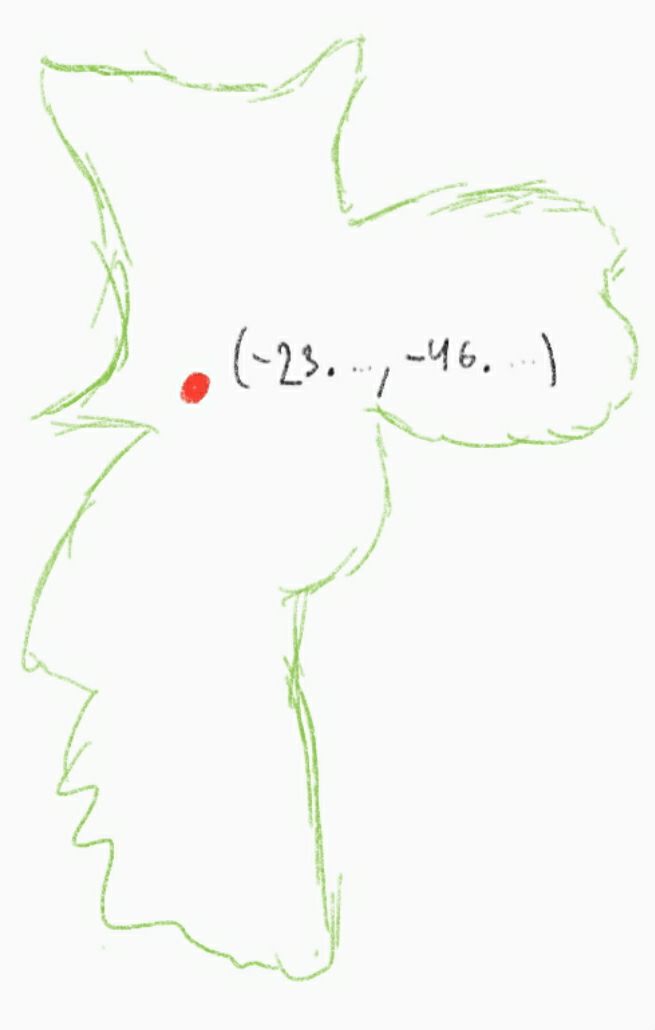
Converting latitude and longitude into coordinates in a plane, where the origin is the center of São Paulo, and using meters as unit;
-
Converting the coordinates in that intermediate plane into another plane, where each X unit corresponds to the width of a page, and each Y unit corresponds to the height of a page. The origin of that plane is the crossing between the most western meridian and most northern parallel represented on the street guide;
-
Converting the plane defined in the step 2 into page numbers and page coordinates;
However, I’ve written it in the following order:
Step 3
Step 3 is quite simple: in the street guide, before the pages that contain the map itself, there is a small map containing its coverage. That map has a grid that shows what page contains each area of the city. Then, we can see where each page is placed and what pages are its neighbors.
Based on that map, I’ve written the matrix contained in the file
pages.py. Note that the matrix pages contains null pages, that represent
areas that aren’t covered by any page in the street guide. This pages matrix
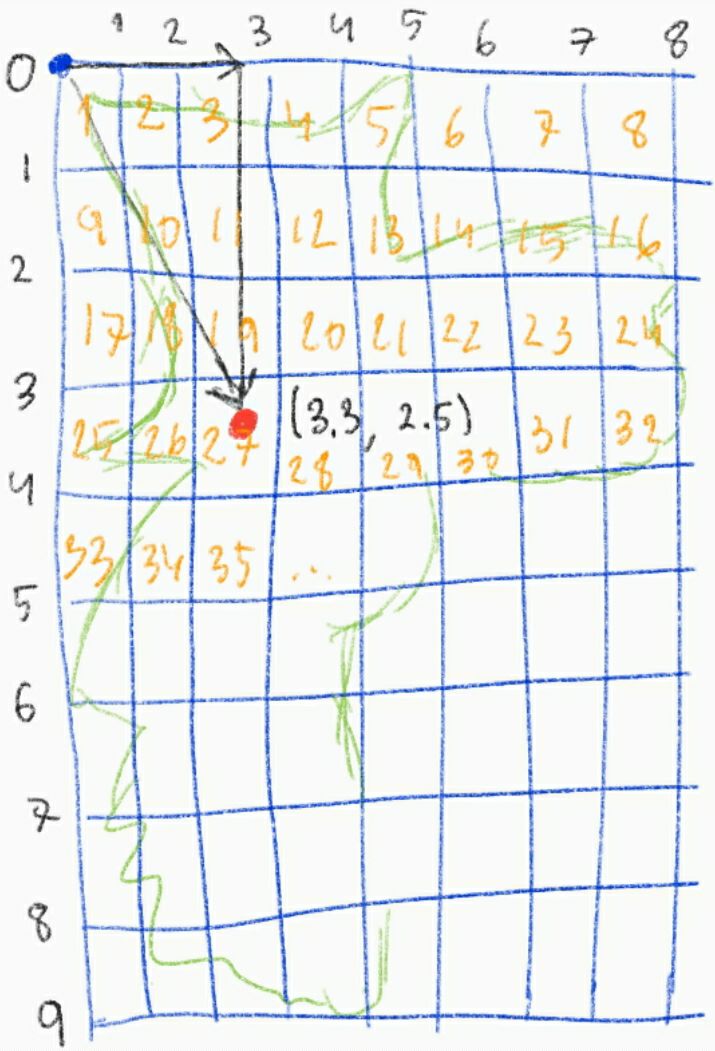
is used to build a Cartesian plane, where the origin is the top-left corner of
the first page of the first row. Actually, the first page of the first row
doesn’t physically exists, however, it doesn’t really matter. Each unit of the X
axis corresponds to the width of a page, and each unit of the Y axis corresponds
to the height of a page.
That way, it is easy to transform a position on the street guide to a position on that Cartesian plane, and also to transform a position in the Cartesian plane to a position in the street guide: Catedral da Sé (a church placed on the center of São Paulo), can be found in the street guide in 151 Z 3. As the page 151 is placed on the row 13 and on the column 15, we can find the integer part of the position on the Cartesian plane: (13, 15). The non-integer part of the coordinates can be calculated after the coordinates inside the page, Z 3. Then, the position of Catedral da Sé on that plane is (13.0834, 15.975).
Step 1
Converting geographical coordinates to meters isn’t straightforward, and in order to do that I needed to make some assumptions.
Assuming that the Earth is a perfect sphere, a degree of latitude has the same length in any place of the planet surface: approximately 10001.965729 km.
The length of a degree of longitude, however, depends on the latitude. The formula for calculating the length in meters of a radian of longitude is given by the following function:
m(lat) = cos(lat) * R
where R is the radius of Earth in meters, and lat is the lattitude in radians.
In order to calculate the average length of a radian of longitude between two
points of different lattitudes, it is enough to divide the integral of m
between the two lattitudes and divide them by the difference between the
lattitudees. Then, we can calculate the average size of a degree, that is:
(π * R / 180) * (sin(π * b/180) - sin(π * a / 180)) / (b - a)
where a and b are the two lattitudes, in degrees.
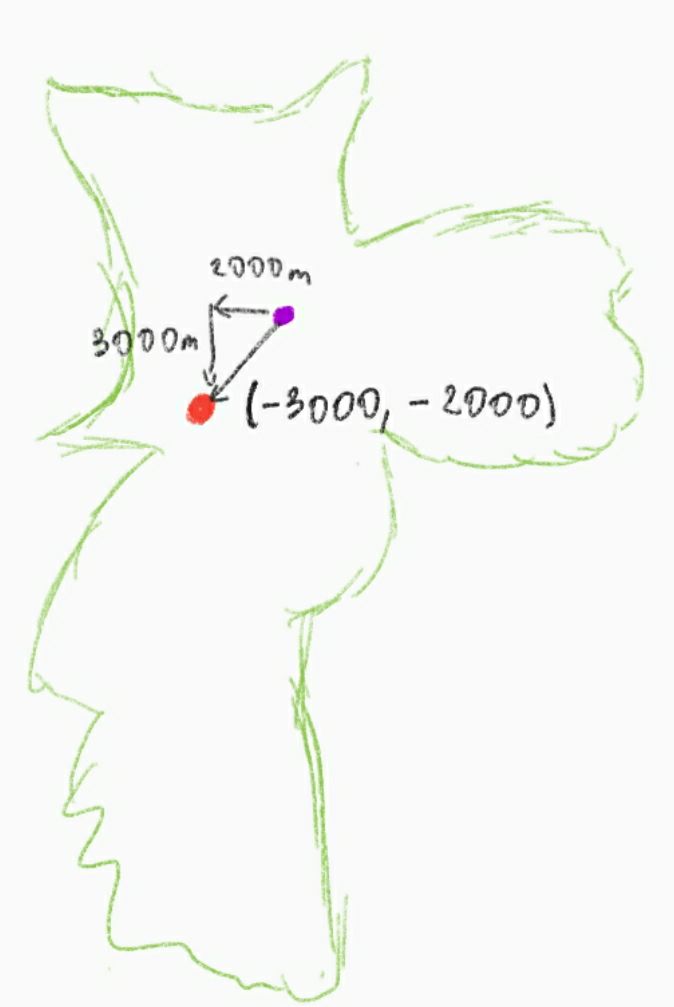
Once calculated the average size of a degree of longitude, it is enough to multiply it by the difference in longitude in order to get the difference in meters from north to south. And it is enough to multiply the length of a degree of lattitude by the difference in lattitude in order to get the difference in meters from west to east.
Here I need to make a second assumption: that the Earth is flat in the city of São Paulo. Just like we did before, that will cause errors, but they are not relevant.
Given that assumption, it is possible to calculate the position of the point relative to the center of São Paulo, in meters. Then, we can place it in a Cartesian plane whose origin is the center of São Paulo, using meter as unit.
Step 2
In the step 3, we defined a carthesian plane that represents the street guide, and in the step 1 we defined a plane using the metric system. Step 2 consists in converting one plane into another, and it is the main conversion step.
The conversion between the two planes is a linear transformation. However, the transformation matrix is unknown.
In order to find the transformation matrix, I took a sample of several points in
the street guide and their geographical coordinates. Those points are in the
file pointset.py. The position of those points was calculated accordingly to
the definitions described before. Given the positions in both planes, it is
possible to perform a linear regression. The linear regression gives us a
transformation matrix that minimizes the error when transforming a plane into
another. Yay!
Execution
Dependencies
- Python 3
- Numpy
How to use
python3 mapo_gps.py
The geographical coordinates should be provided in the decimal notation through
stdin, then it will return the corresponding pages and page coordinates.
Found a mistake ?
This script was written for my personal use, and here I’m only sharing how I did it. I’m not a specialist in GIS, in linear algebra, neither in machine learning.
If you find something wrong in the code or even here, I’ll be happy to hear you in a Github issue or Pull Request.
2023 Update
Three years have passed since I wrote that program. A few months after I wrote the first version of it, I began to work on the backend of delivery company. By coincidence, I was part of a team that maintened the internal geocoding microservice! Deal with maps and geographical coordinates, that here was just for fun, soon after became my routine for the next two years!
For whatever reason, in the step 1 I was reinventing the wheel trying to deduce how to measure distances of geographical coordinates. Nowadays I see that lost a lot of time doing that, and I could just use the Haversine formula, that does exactly that.
Between those three years, I wrote an Android app based on that script. As it is only meant for my personal use, I don’t intend to publish on Play Store. It is nothing more than take the geographical coordinates from GPS, apply the transformation described here, and show the results in the screen. Its source code is on my GitHub, if anyone have interest about it: