Lambdasort

Quicksort implementado apenas com lambdas, em Python

GitHub: https://github.com/lucasoshiro/lambdasort

O cálculo lambda

O Python, assim como várias outras linguagens, suporta funções de alta ordem e funções anônimas. Isto significa, essencialmente, que podemos fazer isso:

# função anônima (lambda). Esta é equivalente à função sqrt:
lambda n: n ** 0.5

# função que recebe função como parâmetro, neste caso, func
def aplica(func, parametro):
    return func(parametro)

# função que devolve outra função, neste caso, fabrica multiplicadores
def fabrica_multiplicador(n):
    return lambda x: n * x

Certo. Com isso as funções são valores, que podem ser criados por outras funções, podem ser devolvidos por outras funções, e que ainda assim podem ser chamadas.

E se escrevermos um código que o tipo de todos os valores sejam funções? Por exemplo:

t = lambda a: lambda b: a
f = lambda a: lambda b: b
x = (lambda a: lambda b: a(b)(f))(t)(f)

Olhando pela primeira vez isso não parece nada útil. Porém, acredite se quiser (spoiler: isso será explicado mais pra frente), mas isso é operação booleana and entre True e False.

O famoso cálculo lambda é isso. Nele temos apenas funções que recebem funções e devolvem funções. Para esse post, isso basta, mas caso queira ler mais sobre, o artigo na Wikipedia sobre o assunto é bem interessante.

Apesar de parecer insuficiente para fazer qualquer coisa, na verdade só com o cálculo lambda conseguimos resolver qualquer problema que seria resolvido com qualquer algoritmo, já que ele é Turing-completo! E quem provou isso foi o próprio Alan Turing!

O excelente Programming with Nothing de Tom Stuart mostra como fazer um fizzbuzz apenas com cálculo lambda em Ruby. Quando conheci o Programming with Nothing fiquei com vontade de fazer algo parecido, e então fiz esta loucura: um QUICKSORT EM CÁLCULO LAMBDA!

Aqui vou contar todas as etapas de como ele foi feito.

O início: um quicksort normal em Python

A primeira etapa foi escrever um quicksort em Python, com uma diferença do quicksort tradicional: ele não altera a lista original, na verdade, ele devolve uma nova lista, assim como a função sorted do Python:

def car(A):
    return A[0]

def cdr(A):
    return A[1:]

def cons(A, x):
    return [x] + A

def concat(A, B):
    return A + B

def quicksort(A):
    if len(A) <= 1: return A
    L, R = partition(A)
    p = car(R)
    L = quicksort(L)
    R = quicksort(cdr(R))
    return concat(L, concat([p], R))

def partition(A):
    p = car(A)

    L, R = [], []

    for x in cdr(A):
        if x < p:
            L, R = cons(x, L), R
        else:
            L, R = L, cons(x, R)

    L, R = L, cons(p, R)

    return L, R

Repare no uso das funções car, cdr e cons. Segui a mesma nomenclatura de Lisp para essas funções. A forma como as listas serão implementadas mais a frente será a mesma de como é implementada em alguns dialetos de Lisp, então tentei me aproximar mais de como as listas funcionam em Lisp do que o usual em em Python:

• A função car devolve o primeiro elemento
• A função cdr devolve uma lista com o resto dos elementos, ou seja, todos os elementos exceto o primeiro.
• Por ora, também implementei cons como uma forma de devolver uma nova lista idêntica mas adicionando um novo elemento ao seu começo, apesar de cons ser mais do que isso (falarei dele mais adiante)
• A função concat concatena duas listas.

De resto, é apenas um quicksort comum:

• A função partition recebe uma lista e separa em duas, sendo a da esquerda com todos os elementos menores que o primeiro elemento da lista da direita (o pivô), e a da direita com todos os elementos maiores ou iguais ao pivô.

• A função quicksort chama partition para separar a lista que será ordenada em duas, e ordena cada uma das duas com o próprio quicksort recursivamente, sendo a base da recursão listas de tamanho menor ou igual a 1.

Quanto às estranhas construções L, R = ..., por enquanto é redundante fazer essa atribuição em paralelo, mas isso nos ajudará no futuro.

Você pode ver isso aqui.

Redefinindo tipos

Como a ideia é reescrever o quicksort apenas com lambdas, precisamos representar os dados de alguma forma usando apenas funções. Os tipos de dados envolvidos aqui são:

• inteiros (os valores dentro da lista que queremos ordenar)
• listas
• pares (para as funções que retornam mais de um valor)
• booleanos (para as verificações)

Felizmente, o próprio criador do cálculo lambda, Alonzo Church, também nos mostrou como fazer isso. A Wikipedia também tem um ótimo artigo sobre isso.

Booleanos

Vamos começar com os mais fáceis, os booleanos:

#boolean constants
LAMBDA_TRUE = lambda a: lambda b: a
LAMBDA_FALSE = lambda a: lambda b: b

#boolean opearations
LAMBDA_OR = lambda a: lambda b: a(LAMBDA_TRUE)(b)
LAMBDA_AND = lambda a: lambda b: a(b)(LAMBDA_FALSE)
LAMBDA_NOT = lambda a: a(LAMBDA_FALSE)(LAMBDA_TRUE)

Sim, o true é só uma função que recebe dois argumentos e devolve o primeiro, e false uma função que recebe dois argumentos e devolve o segundo.

Sei que você está pensando “deveria ser então lambda a, b: a e lambda a, b: b, por que dois lambdas?”. Isso é porque na definição do cálculo lambda, as funções só podem receber um argumento. Ao contrário dessa definição, o lambda em Python pode aceitar zero ou mais argumentos, mas aqui optei por me restringir a só usar funções que recebem um argumento para me manter fiel à definição. Dessa forma, o que seria ser escrito como lambda a1, a2, a3, ..., an: passa a ser escrito como lambda a1: lambda a2: lambda a3: ... lambda an:. Na hora de chamar a função, chamamos com (a1)(a2)(a3)...(an) em vez de (a1, a2, a3, ..., an). O nome dessa conversão é currying, em homenagem a Haskell Curry. Um exemplo de uma linguagem que nativamente usa currying para tratar funções com vários argumentos é Haskell (não me diga…).

Logo em seguida implementei as três operações booleanas básicas:

• not: recebe um booleano de Church, e o chama usando como argumentos false e true. Se o booleano for true, irá devolver o primeiro argumento (false); se for false, devolve o segundo (true).

• or: recebe dois booleanos de church, chama o primeiro passando como argumentos true e segundo booleano. Caso o primeiro argumento do or seja true, devolve seu primeiro argumento (true); caso ele seja false, devolve seu segundo argumento (que é o segundo argumento do or).

• and: bem parecido com o or. Simule ele mentalmente ;-).

Podemos também definir um if:

if

LAMBDA_IF = lambda c: lambda t: lambda e: c(t)(e)

No if, c é a condição; t é o “then”, aquilo que acontece quando a condição é verdadeira, e e é o “else”, o que acontece quando a condição é falsa.

O if então é mais próximo de uma if-expression do Python (ou operador ternário) do que de um if de controle de fluxo:

use_5 = LAMBDA_TRUE
dont_use_5 = LAMBDA_FALSE

a = LAMBDA_IF(use_5)(5)(0) # a = 5
b = LAMBDA_IF(dont_use_5)(5)(0) # a = 0

Conversão

Defini duas funções, para converter os booleanos de Church para os de Python (l2b) e vice-versa (b2l):

#boolean conversion
def l2b(l):
    return l(True)(False)

def b2l(b):
    return LAMBDA_TRUE if b else LAMBDA_FALSE

Exercício mental: simule elas!

Você pode ver isso aqui.

Inteiros

Os numerais de Church são definidos assim:

LAMBDA_ZERO = lambda p: lambda x: x
LAMBDA_ONE = lambda p: lambda x: p(x)
LAMBDA_TWO = lambda p: lambda x: p(p(x))
# etc

Ou seja, todos os inteiros são funções que recebem dois argumentos pe x da seguinte forma:

• 0 é a função que devolve apenas x (igual ao false)
• 1 é a função que devolve p(x)
• 2 é a função que devolve p(p(x))

e assim por diante. Com isso, porém, não conseguimos representar números negativos.

Incremento e decremento

O incremento é bem fácil de definir, é uma função que põe mais uma camada de p(...):

LAMBDA_INCREMENT = lambda l: lambda p: lambda x: p(l(p)(x))

Já o decremento é mais complicado. Explicar ele leva algum tempo, e não acrescenta tanto para nós neste momento saber como ele funciona. Se quiserem ver como funciona, tentem em casa. Se não, só confiem em em mim em Church que isto funciona:

LAMBDA_DECREMENT = lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda y: x)(lambda y: y)

Se você tentou simular isso em casa, tentou ver o que aconteceria se decrementar zero. E viu que o decremento de zero é zero aqui. Infelizmente, essa é uma limitação, e iremos precisar lembrar dela daqui a pouco.

Soma e subtração

Ok, temos então incremento e decremento. Se fizermos n incrementos em um número m, teremos m + n, e se fizermos n decrementos teremos m - n.

Podemos definir soma e subtração assim:

LAMBDA_ADD = lambda m: lambda n: n(LAMBDA_INCREMENT)(m)
LAMBDA_SUB = lambda m: lambda n: n(LAMBDA_DECREMENT)(m)

Repare que o incremento ou decremento será passado como o argumento p do número n e o m será o x. Isto é, m será incrementado ou decrementado com mesma quantidade que chamadas de p que tem em n, e que é justamente n vezes. Muito, muito bonito.

Ainda assim, uma consequência do decremento de zero ser zero aqui é que n - m = 0 sempre que m > n.

Multiplicação e divisão também são possíveis, mas não vão ser úteis para este quicksort.

Comparações

As operações com inteiros que de fato são importantes para o quicksort são as comparações. Vamos começar definindo a função que diz se um numeral de Church é ou não zero (exercício mental: por que isso funciona?):

LAMBDA_EQZ = lambda n: n(lambda x: LAMBDA_FALSE)(LAMBDA_TRUE)

Com apenas a operação de igual a zero, combinada com operações booleanas e aritméticas, conseguimos as outras:

• m <= n: (m - n) == 0 (lembrando que m - n = 0 se n > m)
• m == n: (m <= n) and (n <= m)
• n < m: (m <= n) and not (m == n)

Ou, em Python/cálculo lambda:

LAMBDA_LEQ = lambda m: lambda n: LAMBDA_EQZ(LAMBDA_SUB(m)(n))
LAMBDA_EQ = lambda m: lambda n: LAMBDA_AND(LAMBDA_LEQ(m)(n))(LAMBDA_LEQ(n)(m))
LAMBDA_LESS = lambda m: lambda n: LAMBDA_AND(LAMBDA_LEQ(m)(n))(LAMBDA_NOT(LAMBDA_EQ(m)(n)))

Conversões

Converter o numeral de Church para um inteiro do Python é só passar uma função de incremento como primeiro argumento (o p) e 0 como o segundo:

def l2i(l):
    return l(lambda x: x + 1)(0)

Da mesma forma, podemos fazer o inverso: podemos incrementar varias vezes o zero de Church até chegar no número:

def i2l(i):
    l = LAMBDA_ZERO
    for j in range(0, i):
        l = LAMBDA_INCREMENT(l)

    return l

Também poderemos definir funções para a conversão de listas de inteiros do Python para listas de numerais de Church e vice-versa:

def llist2pylist(L):
    return list(map(l2i, L))

def pylist2llist(L):
    return list(map(i2l, L))

Usando numerais de Church

Como já conseguimos transformar listas de inteiros do Python em listas de numerais de Church e vice-versa, além de que sabemos realizar comparações de numerais de Church, já é possível fazer a primeira alteração no Quicksort:

def quicksort(A):
    if len(A) <= 1: return A
    L, R = partition_wrapper(A)
    p = car(R)
    L = quicksort(L)
    R = quicksort(cdr(R))
    return concat(L, concat([p], R))

def partition_wrapper(A):
    B = pylist2llist(A)
    L, R = partition(B)
    return llist2pylist(L), llist2pylist(R)

def partition(A):
    p = car(A)

    L, R = [], []

    for x in cdr(A):
        if l2b(LAMBDA_LESS(x)(p)):
            L, R = cons(x, L), R
        else:
            L, R = L, cons(x, R)
    L, R = L, cons(p, R)

    return L, R

A função partition passa a operar sobre listas de numerais de Church. Para isso, substituimos x < p por LAMBDA_LESS(x)(p), que devolve um booleano de Church em vez de True ou False. Precisei usar l2b para converter o booleano de Church para booleano de Python, para manter a compatibilidade com o if.

A função partition_wrapper age como um adaptador do novo partition, de forma que recebe inteiros de Python, mas com a partição sendo de fato realizada pelo novo partition.

Farei nas próximas seções várias substituições de tipos, funções e operadores do Python por funções em cálculo lambda, assim como fiz agora. Tentarei só alterar aquilo que for relevante para cada etapa, usando as funções de conversão se for necessário.

Você pode ver isso aqui.

Pares e listas

Nossa estrutura de dados mais básica é o par. O par é, de fato, um par de valores, equivalente a uma tupla do Python de tamanho 2. Na codificaçao de Church, um par e suas operações básicas são definidos assim:

LAMBDA_CONS = lambda a: lambda b: lambda l: l(a)(b)
LAMBDA_CAR = lambda p: p(lambda a: lambda b: a)
LAMBDA_CDR = lambda p: p(lambda a: lambda b: b)

A primeira função, LAMBDA_CONS, define o par. Repare, que ao passar dois valores como seus argumentos, por exemplo, LAMBDA_CONS(15)(20), ela irá devolver uma função que recebe um argumento l e devolve a chamada de l usando os elementos do par como argumentos, no nosso exemplo, l(15)(20). Ou seja: LAMBDA_CONS(15)(20) = lambda l: l(15)(20). Em Python e em outras linguagens que suportam funções de primeira classe esses dois valores ficam armazenados em uma closure, e inclusive, podemos obtê-los assim:

l = LAMBDA_CONS(15)(20)
a, b = (x.cell_contents for x in l.__closure__) # a = 15, b = 20

Quanto às funções LAMBDA_CAR e LAMBDA_CDR, elas devolvem o primeiro e o segundo elemento do par, respectivamente.

Exercício mental: tente entender porque LAMBDA_CAR e LAMBDA_CDR funcionam!

Listas

Se você prestou atenção, reparou que car, cdr e cons é o mesmo nome que das funções que definimos que operam em listas. E de fato, elas são as mesmas! Isso acontece por causa da forma como as listas são implementadas na codificação de Church.

As listas de Church são simplesmente pares em que:

• o primeiro elemento do par é o primeiro elemento da lista
• o segundo elemento é uma lista com o restante dos elementos

Essa é uma definição recursiva em que a base da recursão, ou seja, a lista vazia, pode ser implementada de várias formas. Aqui, usamos para representar a lista vazia o booleano LAMBDA_FALSE:

LAMBDA_EMPTY = LAMBDA_FALSE

Dessa forma, uma lista com os valores [1, 2, 3] é declarada assim:

LAMBDA_CONS(1)(LAMBDA_CONS(2)(LAMBDA_CONS(3)(LAMBDA_FALSE)))

O que, na prática, são pares recursivos, na seguinte forma:

(1, (2, (3, LAMBDA_EMPTY)))

Quantos parênteses! Mas repare que nesse ponto, LAMBDA_CAR, LAMBDA_CDR e LAMBDA_CONS, quando aplicadas a listas, têm o mesmo comportamento das funções car, cdr e cons que definimos para operar em listas do Python:

• LAMBDA_CAR devolve o primeiro elemento do primeiro par, ou seja, o primeiro elemento da lista (1)
• LAMBDA_CDR devolve o primeiro elemento do segundo par, ou seja, o restante da lista ((2, (3, LAMBDA_EMPTY)))
• LAMBDA_CONS adiciona mais um par, acomodando um novo elemento

Como a definição dessas listas é recursiva, a iteração sobre seus ela também será feita de forma recusiva. A função que iremos usar para saber se a recursão chegou ao fim é esta:

LAMBDA_ISEMPTY = lambda l: l(lambda h: lambda t: lambda d: LAMBDA_FALSE)(LAMBDA_TRUE)

Ou seja:

• se l for vazio (é igual a LAMBDA_EMPTY), devolve o segundo argumento: LAMBDA_TRUE

• if l is not empty, then l is a pair. l is called with the function (lambda h: lambda t: lambda d: LAMBDA_FALSE) as argument. That function discards everything and return FALSE. Try to simulate it again ;-).

• se l não for vazio, então l é um par. l é chamada tendo como argumento a (lambda h: lambda t: lambda d: LAMBDA_FALSE). Essa função descarta tudo e devolve LAMBDA_FALSE. Tente simular isso ;-).

Conversão

Pares poderão ser convertidos de e para listas de Python com apenas dois elementos. O jeito pythônico de fazer isto seria com tuplas de apenas dois elementos, mas, para manter a homogeinidade do código, usarei listas:

def l2p(l):
    return [LAMBDA_CAR(l), LAMBDA_CDR(l)]

def p2l(p):
    return LAMBDA_CONS(p[0])(p[1])

Da mesma forma, podemos converter listas de Python e listas de Church:

def ll2pl(l):
    if l2b(LAMBDA_ISEMPTY(l)): return []
    return [LAMBDA_CAR(l)] + ll2pl(LAMBDA_CDR(l))

def pl2ll(l):
    if len(l) == 0: return LAMBDA_EMPTY
    return LAMBDA_CONS(l[0])(pl2ll(l[1:]))

Usando pares de Church no partition

Como a função partition devolve dois valores (uma tupla do Python), podemos usar aqui um par de Church:

    # antes:
    return L, R

    # depois:
    return LAMBDA_CONS(L)(R)

Usando listas de Church no partition

Vamos adicionar listas de Church ao quicksort! Primeiro, vamos converter o partition para operar em listas de Church. A situação atual é esta:

def partition(A):
    p = car(A)

    L, R = [], []

    for x in cdr(A):
        if l2b(LAMBDA_LESS(x)(p)):
            L, R = cons(x, L), R
        else:
            L, R = L, cons(x, R)
    L, R = L, cons(p, R)

    return L, R

Então vamos substitur car, cdr, cons e [] por seus equivalentes em cálculo lambda.

def partition(A):
    p = LAMBDA_CAR(A)
    L, R = LAMBDA_EMPTY, LAMBDA_EMPTY

    for x in lliterator(LAMBDA_CDR(A)):
        if l2b(LAMBDA_LESS(x)(p)):
            L, R = LAMBDA_CONS(x)(L), R
        else:
            L, R = L, LAMBDA_CONS(x)(R)
    L, R = L, LAMBDA_CONS(p)(R)

    return LAMBDA_CONS(L)(R)

Repare que para iterar sobre a lista de Church criei o generator lliterator:

def lliterator(l):
    while not l2b(LAMBDA_ISEMPTY(l)):
        yield LAMBDA_CAR(l)
        l = LAMBDA_CDR(l)

Usando listas de Church no quicksort

Agora vamos adicionar as listas de Church à função quicksort! Ainda precisamos definir a função concat para as listas de Church. Podemos implementá-la de forma recursiva:

• Se a lista à esquerda for vazia, então usamos a da direita
• Se a lista à esquerda não for vazia, devolvemos uma lista em que:
  • o primeiro elemento é o primeiro elemento (car) da lista da esquerda
  • o resto da lista é a concatenação do resto (cdr) da lista da esquerda com a lista da direita

Isso ficaria assim (note o currying):

def LAMBDA_CONCAT(l1):
    def _LAMBDA_CONCAT(l2):
        if l2b(LAMBDA_ISEMPTY(LAMBDA_CDR(l1))):
            return LAMBDA_CONS(LAMBDA_CAR(l1))(l2)
        else:
            return LAMBDA_CONS(LAMBDA_CAR(l1))(LAMBDA_CONCAT(LAMBDA_CDR(l1))(l2))
    return _LAMBDA_CONCAT

Isso fica um tanto distante das outras operações que foram escritas em só uma expressão. Spoiler: vamos tratar isso depois.

Uma vez tendo definida concat, podemos substituir todas as operações sobre listas do Python por operações sobre listas de Church no quicksort:

def quicksort(A):
    # len(A) <= 1
    if l2b(LAMBDA_ISEMPTY(A)): return A
    if l2b(LAMBDA_ISEMPTY(LAMBDA_CDR(A))): return A

    L, R = partition(A)
    p = LAMBDA_CAR(R)

    L = quicksort(L)
    R = quicksort(LAMBDA_CDR(R))

    return LAMBDA_IF(LAMBDA_ISEMPTY(L))(LAMBDA_CONS(p)(R))(LAMBDA_CONCAT(L)(LAMBDA_CONS(p)(R)))

Você pode ver isso aqui.

Transformando laços em funções recursivas

No cálculo lambda, como não temos estados, não podemos fazer laços como em linguagens imperativas, ou seja, repetindo um trecho de código e alterando o estado de alguma variável.

E por não ter estados, em vez de alterar algum valor já existente, devolvemos um novo valor, da mesma forma como fiz ao substituir o comportamento clássico do quicksort para devolver uma lista ordenada em vez de ordernar a lista original.

Mesmo quando estamos em linguagens que implementam tanto o paradigma funcional quanto o imperativo, como Python, se nos restringirmos a escrever um código de forma funcional também não podemos usar laços.

E como fazemos para resolver os problemas que seriam solucionados com laços? Existem várias soluções dependendo do caso, por exemplo, podemos usar reduce, list comprehensions, map, filter, funções recursivas, entre outros. Neste quicksort, temos apenas um laço, na função partition. Iremos substituí-lo por uma função recursiva.

Transformando o for em while

Neste momento, o laço está assim:

p = LAMBDA_CAR(A)
L, R = LAMBDA_EMPTY, LAMBDA_EMPTY

for x in lliterator(LAMBDA_CDR(A)):
    if l2b(LAMBDA_LESS(x)(p)):
        L, R = LAMBDA_CONS(x)(L), R
    else:
        L, R = L, LAMBDA_CONS(x)(R)

Tirando o iterador lliterator e substituindo o for por um while, chegamos nisto:

p = LAMBDA_CAR(A)
L, R = LAMBDA_EMPTY, LAMBDA_EMPTY

S = LAMBDA_CDR(A)
while True:
    if l2b(LAMBDA_ISEMPTY(S)): break
    x = LAMBDA_CAR(S)
    if l2b(LAMBDA_LESS(x)(p)):
        L, R = LAMBDA_CONS(x)(L), R
    else:
        L, R = L, LAMBDA_CONS(x)(R)
    S = LAMBDA_CDR(S)

Ou seja: a princípio a lista S é igual à entrada sem o primeiro elemento (que é o pivô p). Cada iteração do while retira um valor de S e o armazena em x. Caso x < p, x é adicionado ao começo de L e caso contrário é adicionado ao fim de R. A condição de parada é quando a lista S for vazia.

A partir daqui podemos identificar os elementos que serão importantes para escrever este laço como uma função recursiva:

• as entradas L e R são, a princípio, listas de Church vazias;
• a entrada S, a princípio, igual a LAMBDA_CDR(A);
• as saídas, ou seja, os valores de L e R ao final do laço;
• a condição de parada, ou seja, S estar vazia;

Transformando o while em recursão

Legal, partindo do que temos, já conseguimos escrever uma função recursiva (que chamei aqui de _partition), partindo do próprio código do while:

p = LAMBDA_CAR(A)
L, R = LAMBDA_EMPTY, LAMBDA_EMPTY

S = LAMBDA_CDR(A)

def _partition(S, L, R):
    if l2b(LAMBDA_ISEMPTY(S)): return L, R
    x = LAMBDA_CAR(S)
    if l2b(LAMBDA_LESS(x)(p)):
        nL, nR = LAMBDA_CONS(x)(L), R
    else:
        nL, nR = L, LAMBDA_CONS(x)(R)
    S = LAMBDA_CDR(S)
    return _partition(S, nL, nR)

nL, nR = _partition(S, L, R)

Repare que a função _partition não altera o estado das entradas L e R. Em vez de alterar os dados originais, ela devolve novos dados que ficam nas variáveis nL e nR, que são os argumentos L e R da próxima chamada recursiva.

Podemos fazer essa função também devolver pares de Church em vez de tuplas:

p = LAMBDA_CAR(A)
L, R = LAMBDA_EMPTY, LAMBDA_EMPTY

S = LAMBDA_CDR(A)

def _partition(S, L, R):
    if l2b(LAMBDA_ISEMPTY(S)): return LAMBDA_CONS(L)(R)
    x = LAMBDA_CAR(S)
    if l2b(LAMBDA_LESS(x)(p)):
        nL, nR = LAMBDA_CONS(x)(L), R
    else:
        nL, nR = L, LAMBDA_CONS(x)(R)
    S = LAMBDA_CDR(S)
    return _partition(S, L, R)

LR = _partition(S, L, R)
nL, nR = LAMBDA_CAR(LR), LAMBDA_CDR(LR)

Você pode ver isso aqui.

Substituindo variáveis por lets

Uma expressão let permite definir um valor a uma variável dentro de um escopo, de forma que o valor dela nunca seja alterado. Em Python, esse conceito não faz tanto sentido, mas ele é implementado de diferentes formas em diferentes linguagens. Vou mostrar em algumas.

Começando por Kotlin, o let é um método que pode ser usado em qualquer objeto, de forma que a gente pode dar um nome temporário a ele:

val x = 2.let { a -> 
   3.let { b ->
      a + b * a
   }
}

Em Haskell, o let é uma expressão, em que a primeira parte é atribuição dos valores e a segunda é a expressão que queremos obter:

x = let a = 2
        b = 3
    in a + b * a

Em Hy (Python com sintaxe de Lisp), é bastante parecido com Haskell, primeiro atribuimos os valores às variáveis depois declaramos a expressão que irá usá-los:

(setv x
   (let [
      a 2
      b 3
      ]
      (+ a (* b a))
   )
)

(Nos três exemplos, x terá valor 8)

Essa é uma construção bastante usada em linguagens funcionais, já que nelas as variáveis têm um valor fixo dentro de um escopo. Além disso, elas são fáceis de serem escritas usando cálculo lambda. Podemos escrever o exemplo usado nessas três linguagens assim:

def _f(a, b):
   return a + b * a
x = _f(2, 3)

# ou, usando lambda e currying:

x = (lambda a: lambda b: a + b * a)(2)(3)

Repare que, da mesma forma, estamos atribuindo 2 a a e 3 a b, e calculando a + b * a.

A missão dessa etapa é colocar todas as variáveis que não sejam argumentos ou constantes em lets, já que assim elas poderão ser usadas no cálculo lambda.

A partir deste momento, o código começa ficar bastante ilegível, mas vamos focar em um exemplo de como essa substituição é feita, já que as outras substituições são parecidas. Na função _partition que definimos anteriormente, vamos substituir a variável x por um let. No momento essa função está assim:

def _partition(S, L, R):
    if l2b(LAMBDA_ISEMPTY(S)): return LAMBDA_CONS(L)(R)
    x = LAMBDA_CAR(S)
    if l2b(LAMBDA_LESS(x)(p)):
        nL, nR = LAMBDA_CONS(x)(L), R
    else:
        nL, nR = L, LAMBDA_CONS(x)(R)
    S = LAMBDA_CDR(S)
    return _partition(S, L, R)

Como o if serve apenas para mudar o valor de L e R, podemos reescrevê-lo como uma if-expression:

def _partition(S, L, R):
    if l2b(LAMBDA_ISEMPTY(S)): return LAMBDA_CONS(L)(R)
    x = LAMBDA_CAR(S)
    nL, nR = (LAMBDA_CONS(x)(L), R) if l2b(LAMBDA_LESS(x)(p)) else (L, LAMBDA_CONS(x)(R))

    S = LAMBDA_CDR(S)
    return _partition(S, nL, nR)

Como o x só é calculado para ser usado nessa if-expression, podemos usar um let:

• atribuição: x = LAMBDA_CAR(S)
• expressão: a if-expression que acabamos de introduzir

Vamos declarar, para isso, uma nova função _partition2, recebendo como argumento x, e chamá-la logo em seguida, recebendo como argumento x = LAMBDA_CAR(S):

def _partition(S, L, R):
    if l2b(LAMBDA_ISEMPTY(S)): return LAMBDA_CONS(L)(R)

    def _partition2(x):
        return (LAMBDA_CONS(x)(L), R) if l2b(LAMBDA_LESS(x)(p)) else (L, LAMBDA_CONS(x)(R))

    nL, nR = _partition2(LAMBDA_CAR(S))

    S = LAMBDA_CDR(S)
    return _partition(S, nL, nR)

Temos um let! Vamos aproveitar e substituir a tupla por um par de Church:

def _partition(S, L, R):
    if l2b(LAMBDA_ISEMPTY(S)): return LAMBDA_CONS(L)(R)

    def _partition2(x):
        return LAMBDA_CONS(LAMBDA_CONS(x)(L))(R) if l2b(LAMBDA_LESS(x)(p)) else LAMBDA_CONS(L)(LAMBDA_CONS(x)(R))

    LR = _partition2(LAMBDA_CAR(S))
    nL, nR = LAMBDA_CAR(LR), LAMBDA_CDR(LR)

    return _partition(LAMBDA_CDR(S), nL, nR)

Você pode ver isso aqui.

Reescrevendo as funções usando lambda

Neste ponto, feitas todas as substituições de variáveis por let, as funções partition e quicksort já não têm mais variáveis. Elas só têm alguns ifs, a expressão do return e a definição das funções internas usadas para fazer os lets (que têm as mesmas características).

Dê só uma olhada (só uma olhada mesmo, o código já está ilegível):

def quicksort(A):
    if l2b(LAMBDA_ISEMPTY(A)): return A
    if l2b(LAMBDA_ISEMPTY(LAMBDA_CDR(A))): return A

    def _quicksort(A, LR):
        return LAMBDA_IF(LAMBDA_ISEMPTY(quicksort(LAMBDA_CAR(LR))))(LAMBDA_CONS(LAMBDA_CAR(LAMBDA_CDR(LR)))(quicksort(LAMBDA_CDR(LAMBDA_CDR(LR)))))(LAMBDA_CONCAT(quicksort(LAMBDA_CAR(LR)))(LAMBDA_CONS(LAMBDA_CAR(LAMBDA_CDR(LR)))(quicksort(LAMBDA_CDR(LAMBDA_CDR(LR))))))

    return _quicksort(A, partition(A))

def partition(A):
    def _partition(S, L, R, p):
        if l2b(LAMBDA_ISEMPTY(S)): return LAMBDA_CONS(L)(R)
        def _partition2(x, L, R, p):
            if l2b(LAMBDA_LESS(x)(p)): return LAMBDA_CONS(LAMBDA_CONS(x)(L))(R)
            else: return LAMBDA_CONS(L)(LAMBDA_CONS(x)(R))

        def _partition3(S, LR, p):
            return _partition(LAMBDA_CDR(S), LAMBDA_CAR(LR), LAMBDA_CDR(LR), p)

        return _partition3(S, _partition2(LAMBDA_CAR(S), L, R, p), p)

    def _partition4(LR):
        return LAMBDA_CONS(LAMBDA_CAR(LR))(LAMBDA_CONS(LAMBDA_CAR(A))(LAMBDA_CDR(LR)))

    return _partition4(_partition(LAMBDA_CDR(A), LAMBDA_EMPTY, LAMBDA_EMPTY, LAMBDA_CAR(A)))

Podemos substituir esses ifs por if-expressions, e essas if-expressions pelo LAMBDA_IF que criamos com booleanos de Church. Além disso, as funções internas podem ser definidas usando lambda em vez de def, por só terem a expressão de retorno. Chegamos neste código horroroso:

def quicksort(A):
    _quicksort = lambda A: lambda LR: LAMBDA_CONCAT(quicksort(LAMBDA_CAR(LR)))(LAMBDA_CONS(LAMBDA_CAR(LAMBDA_CDR(LR)))(quicksort(LAMBDA_CDR(LAMBDA_CDR(LR)))))

    _quicksort2 = lambda A: LAMBDA_IF(LAMBDA_ISEMPTY(A))(lambda A: A)(lambda A: LAMBDA_IF(LAMBDA_ISEMPTY(LAMBDA_CDR(A)))(A)(_quicksort(A)(partition(A))))

    return _quicksort2(A)(A)

def partition(A):
    _partition2 = lambda x: lambda L: lambda R: lambda p: LAMBDA_IF(LAMBDA_LESS(x)(p))(LAMBDA_CONS(LAMBDA_CONS(x)(L))(R))(LAMBDA_CONS(L)(LAMBDA_CONS(x)(R)))

    _partition3 = lambda S: lambda LR: lambda p: _partition(LAMBDA_CDR(S))(LAMBDA_CAR(LR))(LAMBDA_CDR(LR))(p)

    _partition = (lambda S: LAMBDA_IF(LAMBDA_ISEMPTY(S))(lambda L: lambda R: lambda p: LAMBDA_CONS(L)(R))(lambda L: lambda R: lambda p: _partition3(S)(_partition2(LAMBDA_CAR(S))(L)(R)(p))(p)))

    _partition4 = (lambda A: lambda LR: LAMBDA_CONS(LAMBDA_CAR(LR))(LAMBDA_CONS(LAMBDA_CAR(A))(LAMBDA_CDR(LR))))(A)

    return _partition4(_partition(LAMBDA_CDR(A))(LAMBDA_EMPTY)(LAMBDA_EMPTY)(LAMBDA_CAR(A)))

Neste caso, as funções internas, apesar de terem se tornado variáveis, elas são na verdade constantes. Sendo assim, elas não precisam mais ficar dentro das funções quicksort e partition. Dessa forma, quicksort e partition só teriam a expressão de retorno, logo, também poderiam ser escritas usando lambda em vez de def:

_quicksort = lambda A: lambda LR: LAMBDA_CONCAT(quicksort(LAMBDA_CAR(LR)))(LAMBDA_CONS(LAMBDA_CAR(LAMBDA_CDR(LR)))(quicksort(LAMBDA_CDR(LAMBDA_CDR(LR)))))
_quicksort2 = lambda A: LAMBDA_IF(LAMBDA_ISEMPTY(A))(lambda A: A)(lambda A: LAMBDA_IF(LAMBDA_ISEMPTY(LAMBDA_CDR(A)))(A)(_quicksort(A)(partition(A))))
quicksort = lambda A: _quicksort2(A)(A)
_partition2 = lambda x: lambda L: lambda R: lambda p: LAMBDA_IF(LAMBDA_LESS(x)(p))(LAMBDA_CONS(LAMBDA_CONS(x)(L))(R))(LAMBDA_CONS(L)(LAMBDA_CONS(x)(R)))
_partition3 = lambda S: lambda LR: lambda p: _partition(LAMBDA_CDR(S))(LAMBDA_CAR(LR))(LAMBDA_CDR(LR))(p)
_partition = (lambda S: LAMBDA_IF(LAMBDA_ISEMPTY(S))(lambda L: lambda R: lambda p: LAMBDA_CONS(L)(R))(lambda L: lambda R: lambda p: _partition3(S)(_partition2(LAMBDA_CAR(S))(L)(R)(p))(p)))
_partition4 = (lambda A: lambda LR: LAMBDA_CONS(LAMBDA_CAR(LR))(LAMBDA_CONS(LAMBDA_CAR(A))(LAMBDA_CDR(LR))))
partition = lambda A:_partition4(A)(_partition(LAMBDA_CDR(A))(LAMBDA_EMPTY)(LAMBDA_EMPTY)(LAMBDA_CAR(A)))

Recursão e combinador Y

Algumas dessas funções lambda são recursivas:

• quicksort chama _quickssort2 que chama quicksort
• _partition chama _partition3 que chama _partition

Porém, um dos pontos do cálculo lambda é que uma função não precisa ter nome. Mas como uma função pode referenciar a si mesma sem saber o próprio nome? A resposta para isso é o Combinador Y.

Para ilustrar o combinador Y em ação, vamos usar como exemplo uma função que calcula fatorial:

def fac(n):
   return 1 if n == 0 else n * fac(n-1)

# usando lambda:
fac = lambda n: 1 if n == 0 else n * fac(n-1)

Usamos então, o combinador Y para substituir a chamada de fac:

fac = (lambda f: f(f))(lambda f: lambda n: 1 if n == 0 else n * f(f)(n-1))

# nem precisamos dar o nome fac. Esta expressão calcula 5! = 120 recursivamente:
(lambda f: f(f))(lambda f: lambda n: 1 if n == 0 else n * f(f)(n-1))(5)

O que acontece aí dentro? Repare que temos uma função (lambda f: lambda n: 1 if n == 0 else n * f(f)(n-1)) bastante parecida com a fac original, exceto por receber um argumento f e chamar f(f) em vez de fac. A ideia do combinador Y é que f seja sempre mesma função, e ela passe a si mesma como argumento, recursivamente, para as chamadas recursivas tenham como fazer outras chamadas recursivas. Quem irá garantir a base dessa recursão é (lambda f: f(f)), que vai prover a primeira passagem daquela função para ela mesma.

Exercício mental: simule fac(2), e veja a mágica acontecendo.

Usando o combinador Y

Ok, vamos focar em substituir a chamada recursiva de quicksort pelo combinador Y. A situação no momento é essa:

_quicksort2 = lambda A: LAMBDA_IF(LAMBDA_ISEMPTY(A))(lambda A: A)(lambda A: LAMBDA_IF(LAMBDA_ISEMPTY(LAMBDA_CDR(A)))(A)(_quicksort(A)(partition(A))))
quicksort = lambda A: _quicksort2(A)(A)

Substituindo pelo combinador Y:

_quicksort2 = lambda r: lambda A: LAMBDA_IF(LAMBDA_ISEMPTY(A))(lambda A: A)(lambda A: LAMBDA_IF(LAMBDA_ISEMPTY(LAMBDA_CDR(A)))(A)(_quicksort(r)(A)(partition(A))))
quicksort = (lambda r: r(r))lambda A: _quicksort2(r)(A)(A)

Exercício mental: a chamada de quicksort não está no próprio quicksort, e sim em _quicksort2 (que é chamado por quicksort). Como consegui usar o combinador Y nessa situação?

Você pode ver isso aqui.

Expandindo tudo!

Neste ponto, todos os valores, estruturas de dados e ifs são funções. Além disso, essas e todas as outras funções são valores que podem ser escritos em uma única expressão.

O trabalho aqui é, basicamente, substituir todas as constantes pelos seus valores, de forma que a função quicksort vire uma única expressão. Isso pode ser feito usando a própria substituição de um editor de texto, por exemplo.

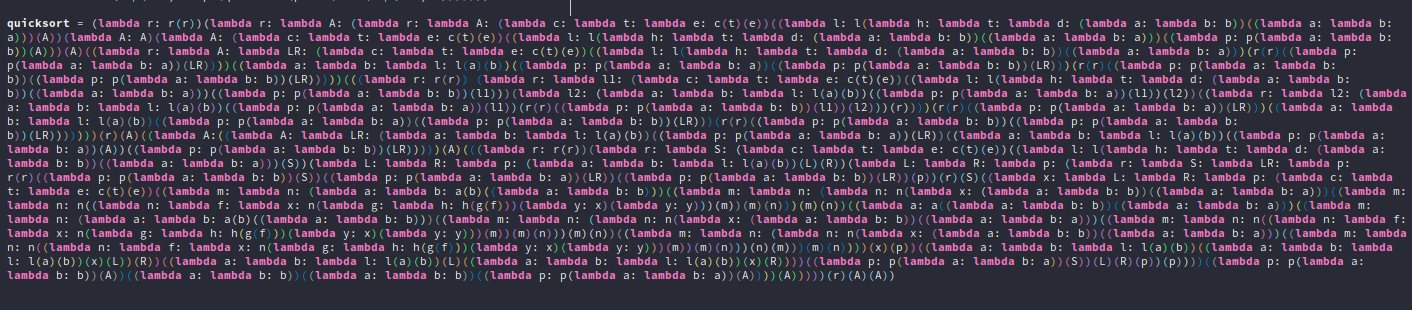
Eis que chegamos nesta coisa horrível:

quicksort = (lambda r: r(r))(lambda r: lambda A: (lambda r: lambda A: (lambda c: lambda t: lambda e: c(t)(e))((lambda l: l(lambda h: lambda t: lambda d: (lambda a: lambda b: b))((lambda a: lambda b: a)))(A))(lambda A: A)(lambda A: (lambda c: lambda t: lambda e: c(t)(e))((lambda l: l(lambda h: lambda t: lambda d: (lambda a: lambda b: b))((lambda a: lambda b: a)))((lambda p: p(lambda a: lambda b: b))(A)))(A)((lambda r: lambda A: lambda LR: (lambda c: lambda t: lambda e: c(t)(e))((lambda l: l(lambda h: lambda t: lambda d: (lambda a: lambda b: b))((lambda a: lambda b: a)))(r(r)((lambda p: p(lambda a: lambda b: a))(LR))))((lambda a: lambda b: lambda l: l(a)(b))((lambda p: p(lambda a: lambda b: a))((lambda p: p(lambda a: lambda b: b))(LR)))(r(r)((lambda p: p(lambda a: lambda b: b))((lambda p: p(lambda a: lambda b: b))(LR)))))(((lambda r: r(r)) (lambda r: lambda l1: (lambda c: lambda t: lambda e: c(t)(e))((lambda l: l(lambda h: lambda t: lambda d: (lambda a: lambda b: b))((lambda a: lambda b: a)))((lambda p: p(lambda a: lambda b: b))(l1)))(lambda l2: (lambda a: lambda b: lambda l: l(a)(b))((lambda p: p(lambda a: lambda b: a))(l1))(l2))((lambda r: lambda l2: (lambda a: lambda b: lambda l: l(a)(b))((lambda p: p(lambda a: lambda b: a))(l1))(r(r)((lambda p: p(lambda a: lambda b: b))(l1))(l2)))(r))))(r(r)((lambda p: p(lambda a: lambda b: a))(LR)))((lambda a: lambda b: lambda l: l(a)(b))((lambda p: p(lambda a: lambda b: a))((lambda p: p(lambda a: lambda b: b))(LR)))(r(r)((lambda p: p(lambda a: lambda b: b))((lambda p: p(lambda a: lambda b: b))(LR)))))))(r)(A)((lambda A:((lambda A: lambda LR: (lambda a: lambda b: lambda l: l(a)(b))((lambda p: p(lambda a: lambda b: a))(LR))((lambda a: lambda b: lambda l: l(a)(b))((lambda p: p(lambda a: lambda b: a))(A))((lambda p: p(lambda a: lambda b: b))(LR)))))(A)(((lambda r: r(r))(lambda r: lambda S: (lambda c: lambda t: lambda e: c(t)(e))((lambda l: l(lambda h: lambda t: lambda d: (lambda a: lambda b: b))((lambda a: lambda b: a)))(S))(lambda L: lambda R: lambda p: (lambda a: lambda b: lambda l: l(a)(b))(L)(R))(lambda L: lambda R: lambda p: (lambda r: lambda S: lambda LR: lambda p: r(r)((lambda p: p(lambda a: lambda b: b))(S))((lambda p: p(lambda a: lambda b: a))(LR))((lambda p: p(lambda a: lambda b: b))(LR))(p))(r)(S)((lambda x: lambda L: lambda R: lambda p: (lambda c: lambda t: lambda e: c(t)(e))((lambda m: lambda n: (lambda a: lambda b: a(b)((lambda a: lambda b: b)))((lambda m: lambda n: (lambda n: n(lambda x: (lambda a: lambda b: b))((lambda a: lambda b: a)))((lambda m: lambda n: n((lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda y: x)(lambda y: y)))(m))(m)(n)))(m)(n))((lambda a: a((lambda a: lambda b: b))((lambda a: lambda b: a)))((lambda m: lambda n: (lambda a: lambda b: a(b)((lambda a: lambda b: b)))((lambda m: lambda n: (lambda n: n(lambda x: (lambda a: lambda b: b))((lambda a: lambda b: a)))((lambda m: lambda n: n((lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda y: x)(lambda y: y)))(m))(m)(n)))(m)(n))((lambda m: lambda n: (lambda n: n(lambda x: (lambda a: lambda b: b))((lambda a: lambda b: a)))((lambda m: lambda n: n((lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda y: x)(lambda y: y)))(m))(m)(n)))(n)(m)))(m)(n))))(x)(p))((lambda a: lambda b: lambda l: l(a)(b))((lambda a: lambda b: lambda l: l(a)(b))(x)(L))(R))((lambda a: lambda b: lambda l: l(a)(b))(L)((lambda a: lambda b: lambda l: l(a)(b))(x)(R))))((lambda p: p(lambda a: lambda b: a))(S))(L)(R)(p))(p))))((lambda p: p(lambda a: lambda b: b))(A))((lambda a: lambda b: b))((lambda a: lambda b: b))((lambda p: p(lambda a: lambda b: a))(A))))(A)))))(r)(A)(A))

Usando o lambdasort

Claro que não podemos usar este quicksort sozinho em uma lista do Python já que ele opera na codificação de Church. Precisaremos então de uma função para traduzir os tipos do Python para a codificação de church, ordernar a lista de Church usando quicksort e então traduzí-la de novo para uma lista doo Python. Vamos fazer isso usando as funções anteriores.

def quicksort_wrapper(A):
    church = pl2ll([i2l(x) for x in A])
    sorted_church = quicksort(church)
    return [l2i(x) for x in ll2pl(sorted_church)]

Agora você pode usar quicksort_wrapper para ordenar uma lista e ele usará por trás o nosso lambdasort:

>>> from lambdasort import quicksort_wrapper
>>> x = [22, 33, 11, 55, 99, 11, 33, 77, 44]
>>> quicksort_wrapper(x)
[11, 11, 22, 33, 33, 44, 55, 77, 99]

Considerações finais

Eu escrevi o lambdasort em 2017 (meu terceiro ano na faculdade) em apenas dois dias bem intensos, depois de ver uma aula do Professor Gubi sobre cálculo lambda e combinador Y. Ele falou sobre o Programming with Nothing, mencionado anteriormente. Eu achei isso tão impressionante que eu quis fazer algo similar, e me desafiei a escrever alguma coisa ainda mais difícil que um fizzbuzz, e aqui estamos!

Escrever ele foi realmente divertido, e eu não reparei no primeiro momento o quanto eu aprendi em apenas dois dias, e ainda levou anos para que eu finalmente escreve este texto explicando o que eu fiz. Então, obrigado por ler até aqui!

Se alguma coisa estiver errada, tanto no texto quanto no código, sinta-se à vontade para abrir uma issue.