Tocando música na impressora 3D
GitHub: https://github.com/lucasoshiro/music2gcode
Como assim?
Os ruídos de motores de passo são causados por suas vibrações. Quantos mais passos um motor de passo fizer por segundo, mais alta será a frequência, consequentemente, mais agudo será o som. Aqui descrevo como que fiz para usá-los para tocar música.
Manipular a frequências de um motor de passo individualmente, quando se tem acesso direto a eles é bastante simples Um exemplo: se eles estiverem conectados a um Arduino através de um driver. Apesar de eu ter montado a minha impressora 3D com um Arduino e drivers de motor de passo, controlar a frequência de rotação de cada motor dela individualmente iria requerer alterações diretas no firmware, o que foge do escopo deste projeto, que visa tocar a música apenas usando um protocolo que normalmente seria usado para impressões 3D comuns.
Para fazer isso, escrevi um programa na linguagem Haskell que recebe como entrada uma música escrita em um formato específico, e devolve como saída comandos no protocolo G-Code que quando executados pela impressora tocam a música em seus motores.
Apesar de o G-Code ser um protocolo universal que vai além das impressoras 3D (também funciona, por exemplo, em cortadoras laser), o foco aqui são apenas as impressoras 3D de filamento com movimentação cartesiana (acredito que sejam as mais comuns…). Não funcionaria por exemplo, em impressoras do tipo Delta.
Entrada
A entrada é uma música descrita em um formato que é uma versão simplificada do que eu defini neste projeto. Do ponto de vista musical, ele é muito básico e pouco flexível em relação aos formatos mais conhecidos, como MIDI, MusicXML, e de programas para notação musical (Finale, Encore, Sibelius, GuitarPro, Musescore, etc), porém, ele é muito fácil de ser escrito por humanos e ser parseado por software. Ele é consiste no seguinte:
TEMPO <bpm>
BEGINCH
<nota 1 do primeiro canal>
<nota 2 do primeiro canal>
...
ENDCH
BEGINCH
<nota 1 do segundo canal>
<nota 2 do segundo canal>
ENDCH
Como é de se imaginar, BEGINCH e ENDCH definem o início e o fim de um
canal. Os canais são tocados simultaneamente.
Cada nota é representada como <nota> <oitava> <duração>, com a nota em forma
anglo-saxônica (CDEFGAB), podendo ter sustenido (#) e bemol (b), e a
duração em unidades de tempo. Dobrados sustenidos, dobrados bemóis, etc, não são
suportados. Silêncios são descritos como - <duração>.
A seguir demonstro como o trecho inicial do chorinho Brejeiro, de Ernesto Nazareth (se você não conhece, ouça aqui no Spotify), escrito na forma de partitura, pode ser transcrito para esse formato:

Saída
A saída são comandos do protocolo G-Code. Mais especificamente, são gerados comandos G0 (Linear Move). Em suma, eles seguem o seguinte formato:
G0 X<posição X> Y<posição Y> Z<posição Z> F<velocidade>
Por exemplo: G0 X10 Y20 Z30 F200 vai mover linearmente o bico de impressão
para a posição (10mm, 20mm, 30mm) a uma velocidade de 200mm/min.
Funcionamento
Ainda tomando como exemplo a partitura de Brejeiro, a conversão ocorre conforme a imagem a seguir. Os números indicam as etapas da conversão:
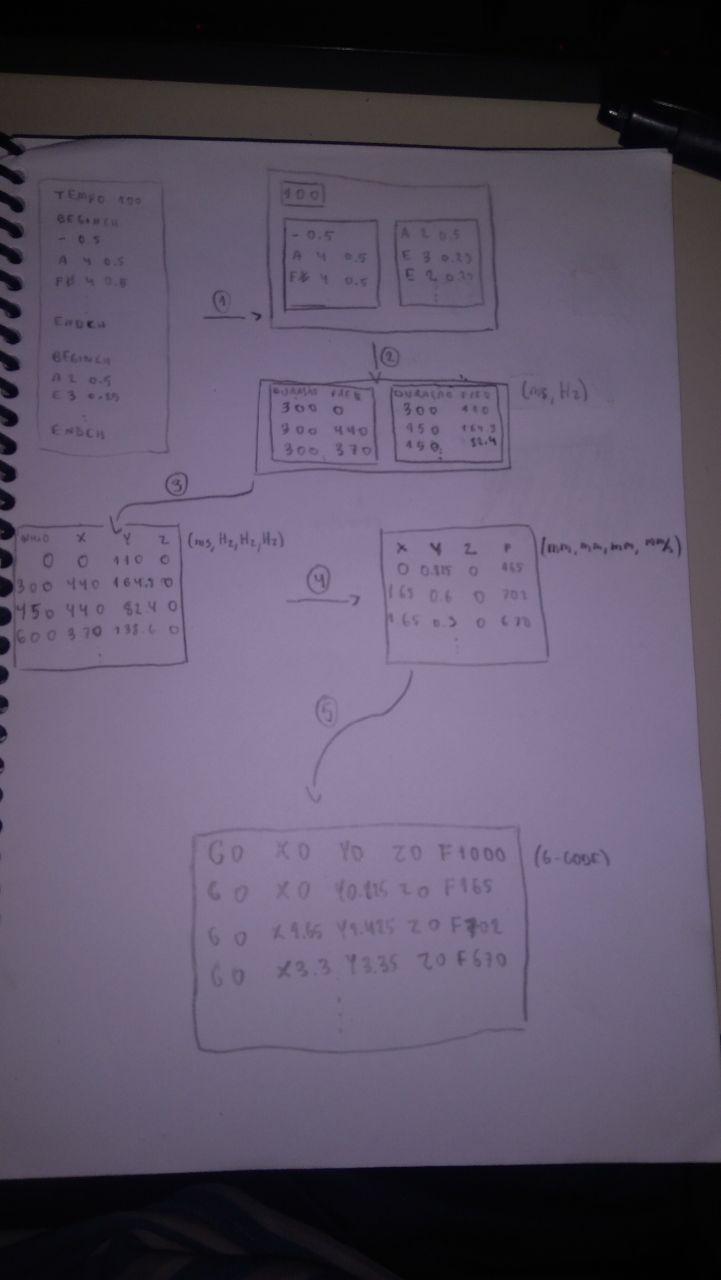
Daqui pra frente explico melhor cada uma delas.
Etapa 1: Parser
Vou pular a implementação do parser por ela ser entediante… Em suma, basta saber que há uma função
parseSong :: [String] -> Song
(ou seja, recebe uma lista de Strings e devolve um Song), em que:
type Hz = Float
type Sec = Float
type Bpm = Int
data SongAtom = Silence Sec | Note (String, Int, Sec)
type Channel = [SongAtom]
type Song = (Bpm, [Channel])
Traduzindo, isso significa que Hz e Sec são apenas tipos de sinômios de
Float e Bpm de Int. Song é, então, composto do andamento da música em bpm
e uma lista de canais, cada canal composto por SongAtoms, que podem ser
silêncios ou notas.
Etapas 2 e 3: Tabela de frequências
Obtendo as frequências
Queremos construir uma tabela com eventos mostrando qual frequência será tocada
por cada eixo em cada instante de tempo tendo como base a música parseada na
etapa anterior. Peço perdão pelo uso do voculário musical aqui, mas não tenho
como fugir dele… De qualquer forma, queremos uma função
freqEventsFromSong, em que:
type FreqEvent = (MiliSec, Hz, Hz, Hz)
freqEventsFromSong :: Song -> [FreqEvent]
Certo. Antes de tudo, precisamos saber como descobrir a frequência de cada nota musical. Baseando-se nesta fórmula contida neste site, podemos fazer uma versão um pouco diferente:
c0 = 16.351597831287418
baseExp = 1.0594630943592953
freq :: SongAtom -> Hz
freq (Silence _) = 0.0
freq (Note n) = mult * c0 * baseExp ** (fromIntegral $ fromFigure figure)
where (figure, octave, _) = n
mult = fromIntegral $ ((2 :: Int) ^ octave)
AAAAAH QUÊ? Bom, a frequência do silêncio obviamente é 0 Hz, então, já deixamos
isso definido hardcoded. c0 é a frequência do Dó 0 (confere
naquele site que eu falei antes), e ela vai ser usado para o cálculo das frequências
de outras notas. O valor mult é o multiplicador da oitava: como a frequência
de uma nota é o dobro de sua oitava inferior, esse multiplicador é 2 ^ oitava.
fromFigure é uma função com a seguinte assinatura:
fromFigure :: String -> Int.
Não vou entrar em detalhes na implementação dela, basta saber que dada uma
nota expressa em uma string (exemplo, A#), ela dá quantos semitons ela tem de
distância em relação ao Dó da mesma oitava (no caso do exemplo, 10). baseExp é
a razão entre a frequência de uma nota e a frequência da nota um semitom abaixo,
ou seja 2^(1/12).
Juntando as duas coisas, calcula-se frequência da nota como mult * c0 *
(baseExp ^ (fromFigure figura)).
Obtendo as durações
Quanto às durações das notas, temos a seguinte função:
period :: Int -> Float -> Sec
period bpm beats = 60 * beats / (fromIntegral bpm)
Em prosa, é uma regra de três: se faz bpm batidas em 60 segundos, quantos
segundos leva para beats batidas.
Juntando os 3 canais em uma tabela
Obtidas então as durações e as frequências de cada nota ou silêncio de cada
canal, precisamos juntar as informações dos três canais em uma só tabela, no
formato descrito no começo desta etapa (uma tabela de FreqEvents).
Por enquanto, temos 3 tabelas, uma para cada canal, cujas colunas são (Duração,
Frequência). Como saber quando cada nota irá iniciar? Simples, como dentro de
cada canal elas são sequenciais, o início dela é igual à soma da duração de
todas as notas anteriores.
Com isso, pode-se juntar da seguinte forma: cada entrada na tabela indica quando
há uma alteração de frequência em um dos canais, contendo a frequência nova, e
copiando a frequência anterior dos outros canais. Assim, conseguimos chegar no
resultado esperado de freqEventsFromSong
Etapa 4: Variações de posição e velocidade
Nesta etapa, queremos pegar a saída da etapa anterior e usá-la para descobrir o
quanto e em que velocidade cada eixo deverá se mover a fim de obter as notas, ou
seja, a função fromFreqEvents em que:
type MM = Float
type MM_s = Float
type Movement = (MM, MM, MM, MM_s)
fromFreqEvents :: Printer -> [FreqEvent] -> [Movement]
em que Printer carrega informações sobre a impressora, [FreqEvent] é a lista
de eventos da etapa anterior e [Movement] é uma lista de movimentos
resultantes.
Como eu disse anteriormente, a variação de nota pelos motores ocorre com a
frequência que eles são movimentados. E a duração? Bom, isso é fácil, nós apenas
precisamos multiplicar a frequência pela duração, com p = Δt * f, em que p é
o número de passos, Δt é a duração e f é a frequência. Por exemplo: se temos
uma nota de 440Hz tocada por dois segundos, então significa que devemos mover
880 passos o motor a 440Hz.
E como eu disse anteriormente, não temos o controle disso diretamente por
G-Code, porém, podemos controlar quantos milímetros cada eixo irá se mover,
e a velocidade dessa movimentação, em milímetros por minuto. E como calular
isso? Bom, simples, para cada eixo, a posição pode ser calculada com a fórmula
Δs = p * (pmm) em que p é o número de passos e pmm é o número de passos
necessários para que o eixo se mova 1mm.
O cálculo da velocidade precisa ser feito em conjunto com os três
eixos. Lembrando de física, a velocidade para cada eixo deveria ser calculada
como v = Δs / Δt. Mas como a velocidade que deve ser fornecida no G-Code é a
norma da soma vetorial das velocidades dos três eixos, o Δs deverá ser a norma
da soma vetorial dos deslocamentos de cada eixo. Ou, em outras palavras:
Δs = sqrt (Δsx² + Δsy² + Δsz²).
Feito isso, é nessário fazer as conversões de unidade da velocidade, uma vez que estávamos trabalhando com milímetros e milisegundos e o G-Code trabalha com milímetros por minuto.
Etapa 5: Posicionamento absoluto e G-Code
Esta é a última etapa, e é a mais delicada. Até agora, temos uma tabela que nos diz quantos mílimitros cada eixo deverá se mover, e a velocidade do movimento. O que queremos, no G-Code, é a posição absoluta para onde a impressora deverá movimentar a extrusora. Para isso, é necessário tomar cuidado para que os movimentos sejam todos feitos dentro do espaço de impressão, caso contrário, além de não funcionar poderá trazer danos à impressora.
Em termos de código, queremos uma função assim:
fromRelativeMovements :: Printer -> [Movement] -> GCode
ou seja, recebe informações sobre a impressora (no caso, o que importa aqui são os limites de cada eixo), a lista de movimentos relativos mencionados da etapa anterior, e devolve o G-Code resultante.
A primeira posição é o ponto de partida para a sequência de movimentos seguintes, e está definida assim:
fstPos = (x0, y0, z0, homeSpeed)
A partir de uma posição, podemos calcular a posição seguinte, recursivamente. Bom, tendo em mãos essa primeira posição, e a lista de movimentos relativos, podemos calcular as posições absolutas assim:
absolutes = foldl nextSafeMovement [fstPos] movements
where nextSafeMovement l d = l ++ nextSafeMovements printer (last l) d
Ou em português: a aplicação da função nextSafeMovements tendo como argumentos
printer (as informações da impressora), uma posição absoluta, e a posição
relativa referente ao próximo movimento relativo devolve quais são as posições
necessárias para o cumprimento desse movimento. Bom, um pouco confuso, sim. O
que o ocorre aqui é que um único movimento relativo poderá ser convertido em
mais de um movimento absoluto, já que ele poderá ser “quebrado” em dois
movimentos ou mais caso ele extrapole os limites da impressora.
Tá, mas e o que é nextSafeMovements? Bom, uma função
com essa assinatura:
nextSafeMovements :: Printer -> Position -> Movement -> [Position]
ou seja, nada além do mencionado anteriormente, recebe as informações da impressora, a última posição absoluta calculada, o movimento relativo que se quer aplicar, e devolve uma lista de posições relativas.
O funcionamento interno dessa função é um pouco longo para ser descrito em mais detalhes aqui, porém, basta saber que:
-
o sentido da movimentação de cada eixo escolhido é o que se move em direção à borda mais distante do eixo, dando mais espaço para a movimentação;
-
caso haja espaço suficiente para fazer um só movimento, ele é o que será usado;
-
caso não haja, a movimentação será feita até encontrar com uma borda. A posição resultante e o movimento relativo restante é usado como parâmetros da aplicação da mesma função. Essa chamada recursiva é feita até que não haja mais movimento relativo restante;
-
a velocidade é sempre a mesma calculada no movimento relativo, não é necessário alterar ela em nada.
Temos então uma lista de para quais posições cada eixo deverá se movimentar, e qual a velocidade que eles devem se mover para cada posição. Isso, em si, já são os parâmetros do comando G0 do G-Code, ou seja, basta formatálos como descrito láááááá no começo desse post.
Enfim, G-Code
Já temos então o G-Code, que poderá ser colocado em um cartão de memória, ou enviado para a impressora através do software de sua preferência.
Possíveis features para o futuro
- Mostrar a letra da música no display da impressora
- Usar o motor da extrusora como um canal extra
- Usar o buzzer como um canal extra
- Adicionar suporte a impressoras dos tipos Delta e CoreXY
2023 Update
Faltou um video disso funcionando. Aqui vai ele:
2023 Update #2
Atendando a pedidos, eu adicionei suporte para tablaturas do GuitarPro como entrada. Isso foi feito em uma tarde, então pode estar bem bugado ainda. Porém, é um grande avanço, já que é mais fácil editar nele do que no formato que eu descrevi acima.
Esse novo código funciona como o parser descrito na etapa 1.